🌟有限元分析学习笔记（一）：刚度矩阵的推导与组装

完成时间：2021.12.28
感谢 江南大学胡清元 老师的讲解
参考：

• 《有限单元法》-- 王勖成

• 平面四边形单元有限元实现——有限元实践笔记（6）

• 有限元分析：ANSYS理论与应用 第四版

• 四节点矩形单元有限元分析过程

前言

本人是信息与计算科学专业的大四学生，因工作和毕业论文需要，所以学习有限元，本人除了高中物理以外没有任何其他力学基础，所以这是一篇纯数学和程序员向的有限元笔记，与网上其他教程不同，除去了有限元中繁冗复杂的力学方程和物理条件，只剩下数学推导和少部分的物理方程，不妥之处可以发送内容到邮箱：hi@qiql.net, 阅读本文需要你有以下学科知识：微积分、线代、数值分析 或了解以下知识点：求导、微分、链式法则、矩阵乘法、求逆、插值、二维积分、雅可比矩阵、数值积分(高斯积分)。

假如读者与我一样，无力学背景，建议读者在掌握了上述前两个知识点的情况下，先看 有限元分析：ANSYS理论与应用 第四版 这本书中的绪论部分中的第一个例子（必须能完全理解该例子，物理过程不难，有初中物理基础即可），了解一下有限元的基本思想；然后阅读《有限单元法》-- 王勖成 书中的第一章和第二章，这本书若无力学基础，读来十分晦涩，可连滚带爬往前阅读，无需过多在意其中复杂的物理方程；然后带着无尽的疑惑阅读四节点矩形单元有限元分析过程，该文为PPT，可能读者访问时链接已失效，可以向我邮件求助，该PPT讲的十分清晰，但其中的雅克比变换有些不符合常规；理清思路后，结合本文和平面四边形单元有限元实现——有限元实践笔记（6） 一起阅读，慢慢理解，注意：本文与后者中的符号有些许不同，十分容易造成阅读混乱，逻辑不清晰，读者需要仔细认真推导其中方程，不断搜索与查找，不能只看不写，哪怕抄一抄也是极好的，且后者中的雅克比矩阵部分有一些错误，推导时注意规避。

一、设位移函数

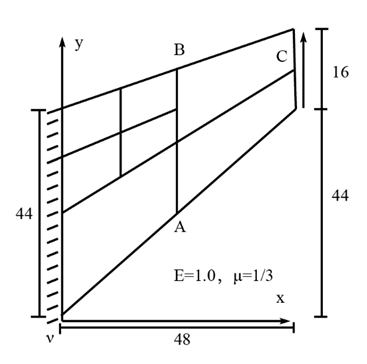
考虑如图 1 的Cook短斜梁问题：

图1 Cook 短斜梁
对其进行离散化，假如划分后的网格中的某单元如图 2 所示：

假如单元节点序号如图2所示：

图2 Cook 短斜梁中的一个单元

对于平面上的四节点单元，每个结点有两个自由度

$$\bold a_i= \left( \begin{array}{ccc} \bold u_i\\ \bold v_i\\ \end{array}\tag{1.0} \right)$$

即一共有 8 个结点位移

$$\bold a^e= \left( \begin{array}{ccc} \bold a_i\\ \bold a_j\\ \bold a_m\\ \bold a_n\\ \end{array} \right) =\begin{bmatrix} u_i & v_i & u_j & v_j & u_m & v_m & u_n & v_n\\ \end{bmatrix}^T$$

设位移函数为：

$$\begin{cases} u = \beta_1+\beta_2\cdot x + \beta_3\cdot y+\beta_4\cdot x \cdot y\\ v = \beta_5+\beta_6\cdot x + \beta_7\cdot y+\beta_8\cdot x \cdot y\\ \end{cases}$$

或者，写为：

$$\{\delta(x,y)\}= \begin{bmatrix} f(x,y)\\ \end{bmatrix} \cdot \{\bold\beta\}$$

整理，得到：

$$\begin{bmatrix} u_i\\ v_i\\ u_j\\ v_j\\ u_m\\ v_m\\ u_n\\ v_n\\ \end{bmatrix} = \underbrace{ \begin{bmatrix} 1 &x_i & y_i & x_i\cdot y_i & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 &x_i & y_i & x_i\cdot y_i\\ 1 &x_j & y_j & x_j\cdot y_j & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 &x_j & y_j & x_j\cdot y_j\\ 1 &x_m & y_m & x_m\cdot y_m & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 &x_m & y_m & x_m\cdot y_m\\ 1 &x_n & y_n & x_n\cdot y_n & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 &x_n & y_n & x_n\cdot y_n\\ \end{bmatrix} }_{设为\bold A_{(8*8)}} \cdot \begin{bmatrix} \beta_1\\ \beta_2\\ \beta_3\\ \beta_4\\ \beta_5\\ \beta_6\\ \beta_7\\ \beta_8 \end{bmatrix}$$

二、求解位移函数中的未知量

得到了 $\bold a^e=\bold A \cdot \beta$ 后解之，得

$$\{\beta\}= \bold A ^{-1} \cdot \bold a^e \tag 6$$

将（6）式代入（4）中，得到：

$$\{\delta(x,y)\}= \begin{bmatrix} f(x,y)\\ \end{bmatrix} \cdot \{\bold\beta\} = \begin{bmatrix} f(x,y)\\ \end{bmatrix} \underbrace{ \cdot \bold A^{-1}\cdot \bold a^e }_{ \{\beta\}} =[N(x,y)]\cdot \bold a^e \tag 7$$

整理，得到：

$$\{\delta(x,y)\}= \begin{bmatrix} u\\ v \end{bmatrix} = \begin{bmatrix} N_i & 0 & N_j & 0 & N_m & 0 & N_n & 0\\ 0 & N_i & 0 & N_j & 0 & N_m & 0 & N_n \end{bmatrix} \cdot \begin{bmatrix} u_i\\ v_i\\ u_j\\ v_j\\ u_m\\ v_m\\ u_n\\ v_n\\ \end{bmatrix}$$

其中，N(x,y) 就是 形函数，或称之为 插值函数

三、形函数的性质

• 性质一

$$N(x_i,y_i)=\delta_{ij}= \begin{cases} 1&,j=i\\ 0&,j\neq i \end{cases}$$

• 性质二

$$\sum_i N_i(x,y)=N_i(x,y)+N_j(x,y)+N_m(x,y)+N_n(x,y) = 1$$

​ 即，在单元内的任意一个位置，形函数的和均为 1

在本文中，因为单元是四个结点

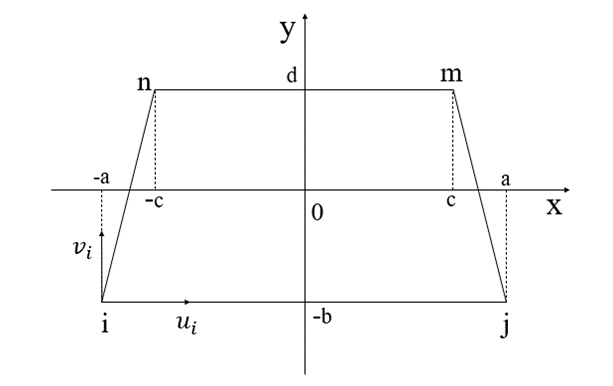
假如，四个结点的坐标为：

结点序号	x坐标	y坐标
$i$	$-a$	$-b$
$j$	$a$	$-b$
$m$	$c$	$d$
$n$	$-c$	$d$

表1，四节点单元的坐标

那么，形函数为：

$$\left\{ \begin{aligned} N_i(x,y) & = \frac{1}{4} \cdot (1-\frac{x}{a})\cdot (1-\frac{y}{b})\\ N_j(x,y) &= \frac{1}{4} \cdot (1+\frac{x}{a})\cdot (1-\frac{y}{b})\\ N_m(x,y) &= \frac{1}{4} \cdot (1+\frac{x}{c})\cdot (1+\frac{y}{d})\\ N_n(x,y) &= \frac{1}{4} \cdot (1-\frac{x}{c})\cdot (1+\frac{y}{d}) \end{aligned} \right.$$

至此，整理，得到：

$$\begin{aligned} & u=N_i(x,y)\cdot u_i + N_j(x,y) \cdot u_j + N_m(x,y) \cdot u_m + N_n(x,y) \cdot u_n\\ & v=N_i(x,y)\cdot v_i + N_j(x,y) \cdot v_j + N_m(x,y) \cdot v_m + N_n(x,y) \cdot v_n \end{aligned}$$

因为式中的 $u_i,v_i(i,j,m,n)$ 是常数，所以位移函数是完全由形函数来决定的

对得到的形函数，验证形函数的性质（1）和性质（2）

• 验证性质（1）： $N(x_i,y_i)=\delta_{ij}= \begin{cases} 1&,j=i\\ 0&,j\neq i \end{cases}$

$$\left\{ \begin{aligned} N_i(x_i,y_i)&=\frac{1}{4} \cdot (1-\frac{-a}{a})\cdot (1-\frac{-b}{b}) = 1\\ N_i(x_j,y_j) &=\frac{1}{4} \cdot (1-\frac{a}{a})\cdot (1-\frac{-b}{b}) = 0\\ N_i(x_m,y_m) &=\frac{1}{4} \cdot (1-\frac{-c}{a})\cdot (1-\frac{d}{d}) = 0\\ N_i(x_n,y_n) &=\frac{1}{4} \cdot (1-\frac{c}{a})\cdot (1-\frac{d}{d}) = 0 \end{aligned} \right.$$

对于结点 $j,m,n$ 同理

• 验证性质（2）： $\sum_i N_i(x,y)=N_i+N_j(x,y)+N_m(x,y)+N_n(x,y) = 1$

$$\begin{aligned} \sum_i N_i(x,y) & =N_i+N_j(x,y)+N_m(x,y)+N_n(x,y)\\ &=\frac{1}{4} \cdot (1-\frac{x}{a})\cdot (1-\frac{y}{b})+ \frac{1}{4} \cdot (1+\frac{x}{a})\cdot (1-\frac{y}{b})+ \frac{1}{4} \cdot (1+\frac{x}{c})\cdot (1+\frac{y}{b})+ \frac{1}{4} \cdot (1-\frac{x}{c})\cdot (1+\frac{y}{b})\\ & = \frac{1}{4} \cdot[ (1-\frac{y}{b})(1-\frac{x}{a}+1+\frac{x}{a})+(1-\frac{y}{b})(1+\frac{x}{c}+1-\frac{x}{c})]\\ & = \frac{1}{4} \cdot [(1-\frac{y}{b})\cdot2 + (1+\frac{y}{b}\cdot 2)\\ & =1 \end{aligned}$$

为方便后文叙述，以及符号规范，令 $\bold u = \begin{bmatrix}u\\ v \end{bmatrix}$ 即：用 $\bold u$ 表示位移

综上，得到：

$$\bold u = \bold N \cdot \bold a^e$$

其中：

$$\bold N = \begin{bmatrix} N_i(x,y) & 0 & N_j(x,y) & 0 & N_m(x,y) & 0 & N_n(x,y) & 0\\ 0 & N_i(x,y) & 0 & N_j(x,y) & 0 & N_m(x,y) & 0 & N_n(x,y)\\ \end{bmatrix}$$

四、根据几何方程求应变矩阵

几何方程的矩阵形式为：

$$\bold \epsilon =\bold L\bold u$$

其中， $\bold L$ 为微分算子， $\bold u$ 为位移，在二维条件下，其值为：

$$\bold L =\begin{bmatrix} \frac{\partial}{\partial x} & 0\\ 0 & \frac{\partial}{\partial y}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y}\\ \end{bmatrix} =A^T$$

若是在三维条件下，其值为：

$$\bold L =\begin{bmatrix} \frac{\partial}{\partial x} & 0 & 0\\ 0 & \frac{\partial}{\partial y} & 0\\ 0 & 0 & \frac{\partial}{\partial z}\\ \frac{\partial}{\partial y} & \frac{\partial}{\partial x} & 0\\ 0 & \frac{\partial}{\partial z} & \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z} & 0 & \frac{\partial}{\partial x}\\ \end{bmatrix} =A^T$$

根据（11）式、（13）式、（14）式，本文所研究问题（二维平面应力问题）的几何方程为：

$$\{\bold \epsilon \}= \begin{pmatrix} \epsilon_x \\ \epsilon_y \\ \gamma_{xy} \end{pmatrix} = \underbrace{ \begin{bmatrix} \frac{\partial}{\partial x} & 0\\ 0 & \frac{\partial}{\partial y}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y}\\ \end{bmatrix} \cdot \bold N }_{\bold B} \cdot \bold a^e =\bold B\cdot \bold a^e$$

其中：

• $\gamma_{xy}$ 是剪应变 $\epsilon_x$ 和 $\epsilon_y$ 分别是 $x$ 和 $y$ 方向的正应变
• $\bold N$ 为形函数矩阵（2*8）, 其值为：

$$\bold N = \begin{bmatrix} N_i & 0 & N_j & 0 & N_m & 0 & N_n & 0\\ 0 & N_i & 0 & N_j & 0 & N_m & 0 & N_n \end{bmatrix}$$

将其进行分块，不妨写为：

$$\begin{aligned} & \begin{bmatrix} \bold N_i & \bold N_j &\bold N_m &\bold N_n\\ \end{bmatrix} & 其中，\bold N_i= \begin{bmatrix} N_i & 0\\ 0 & N_i \end{bmatrix} & ,\;\;\; (i,j,m,n) \end{aligned}$$

其中，

• $\bold a^e$ 为单元位移列阵， $\bold B$ 即为应变矩阵，对形函数矩阵 $\bold N$ 求微分，即可得到 $\bold B$
• 显然，对 $\bold N$ 进行分块后，对 $\bold B$ 也可以进行分块，不妨写为：

$$\begin{aligned} & \bold B = \bold L \cdot \bold N = \begin{bmatrix} \bold B_i & \bold B_j &\bold B_m &\bold B_n\\ \end{bmatrix} & 其中，\bold B_i= \begin{bmatrix} \frac{\partial}{\partial x} & 0\\ 0 & \frac{\partial}{\partial y}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y}\\ \end{bmatrix} \begin{bmatrix} N_i & 0\\ 0 & N_i \end{bmatrix} =\bold L \cdot \bold N_i & \;,\;\;(i,j,m,n) \end{aligned}$$

五、根据物理方程求应力矩阵

弹性力学中，将应力与应变之间的转换关系也称为弹性关系。对于各向同性的线弹性材料，应力通过应变的表达式可用矩阵形式表示为：

$$\bold \sigma = \bold D \cdot \epsilon$$

其中，$\epsilon$ 为应变矩阵，$\sigma$ 为应力矩阵，D 为弹性矩阵

$$\bold D =\frac{E \cdot (1-\nu)}{(1+\nu)\cdot (1-2\nu)} =\begin{bmatrix} 1 & \frac{\nu}{(1-\nu)} & \frac{\nu}{(1-\nu)} & 0 & 0 & 0\\ \frac{\nu}{(1-\nu)} & 1 & \frac{\nu}{(1-\nu)} & 0 & 0 & 0\\ \frac{\nu}{(1-\nu)} & \frac{\nu}{(1-\nu)} & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} & 0 & 0\\ 0 & 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} \end{bmatrix}$$

如你所见，$\bold D$ 是一个对称阵，作为弹性矩阵，它完全取决于弹性体材料的弹性模量 $E$ 和泊桑比 $\nu$ 。

另外，此矩阵还有另一种表示方式，也可以采用拉梅常数 $G$ 和 $\lambda$ ，它们和 $E$，$\nu$ 的关系如下

$$\begin{aligned} &G=\frac{E}{2(1+\nu)}\;\;\; &\lambda = \frac{E\nu}{(1+\nu)(1-2\nu)} \end{aligned}$$

$G$ 也称为剪切弹性模量，注意到：

$$\lambda + 2 G = \frac {E(1-\nu)}{(1+\nu)(1-2\nu)}$$

故弹性矩阵 $\bold D$ 亦可以表示为：

$$\bold D =\begin{bmatrix} \lambda + 2G & \lambda & \lambda & 0 & 0 & 0\\ \lambda & \lambda + 2G & \lambda & 0 & 0 & 0\\ \lambda &\lambda & \lambda + 2G & 0 & 0 & 0\\ 0 & 0 & 0 & G & 0 & 0\\ 0 & 0 & 0 & 0 & G & 0\\ 0 & 0 & 0 & 0 & 0 & G\\ \end{bmatrix}$$

所以，物理方程的另一种形式是：

$$\epsilon = \bold C \sigma$$

其中， $\bold C$ 是柔度矩阵，它和弹性矩阵是互逆关系

注意：本文中在求解应力矩阵时，暂不采用柔度矩阵的方式

根据《有限单元法》一书中第 61 页的说明：

• 对于平面应力问题：

$$\begin{aligned} & E_0=E & \nu_0 = \nu \end{aligned}$$

• 对于平面应变问题：

$$\begin{aligned} & E_0=\frac{E}{1-\nu^2} & \nu_0=\frac{v}{1-\nu} \end{aligned}$$

综上，求得 $\bold D$ 矩阵为：

$$\bold D = \frac{E_0}{1-\nu_0^2}\cdot \begin{bmatrix} 1 & \nu_0 & 0 \\ \nu_0 & 1 &0 \\ 0 & 0 & \frac{1-\nu_0}{2} \end{bmatrix}$$

那么：

$$\{\sigma\} = [\bold D]\cdot\{\epsilon\} = \underbrace{ [\bold D]\cdot [\bold B] }_{[\bold S]} \cdot\{\bold a^e\}=[\bold S]\cdot \{\bold a^e\}$$

其中， $\bold S$ 即为应力矩阵

由于， $\bold B$ 可以写为分块矩阵，所以 $\bold S$ 也可以写为下面形式的分块矩阵：

$$\begin{aligned} & \bold S = \bold D \cdot \bold B= \begin{bmatrix} \bold S_i & \bold S_j &\bold S_m &\bold S_n\\ \end{bmatrix} & 其中，\bold S_i =\bold D \cdot \bold B_i & \;,\;\;(i,j,m,n) \end{aligned}$$

注意： $\bold S$ 与 $\bold B$ 相同，也都是常量阵，但在很多情况下，不单独定义应力矩阵 $\bold S$ ，而直接用 $\bold D\bold B$ 去计算应力

六、转换单元坐标系

虚功原理这块比较复杂，但结论是：

$$\bold K^e=\iint\limits_{A}\bold B^T\cdot \bold D \cdot \bold B \cdot t \;\;\mathrm{d}x\mathrm{d}y$$

其中， $t$ 为单元的厚度，$\bold K^e$ 是单元刚度阵

如果要直接在单元内进行积分，由于各个单元的形状、大小不仅相同，求解起来变得复杂，而且工程问题也不一定非要取得精确解，有误差可控的数值解就可以了，如果能将积分区域规定到一个固定的区域内，就可以采用很多现有的数值积分方法来进行快速求解，具体的说，就是致力于寻找一个映射，将原来的单元，无论形状如何，都可以映射到一个基准单元中，积分区域将由原来的单元转变为基准单元。（这段是我自己的理解）

在正式推导之前，我们需要更改原来的形函数，之前在划分单元后，每个单元的形状都不尽相同，所以位移插值函数也不同，求解效率低，通过将形状不规整的实际单元和形状规整的标准单元之间建立坐标映射关系，在标准单元上去研究它的性质，却不改变原来的问题，映射称为参数映射，单元称为参数单元，如果坐标变换和试函数里的形函数、插值节点完全相同，则变换就称为等参数变换，参数单元称等参数单元。相应的还有亚参元和超参元。^[1]

一种粗暴的变换方式是直接进行压缩，如这篇：https://www.docin.com/p-764314942.html

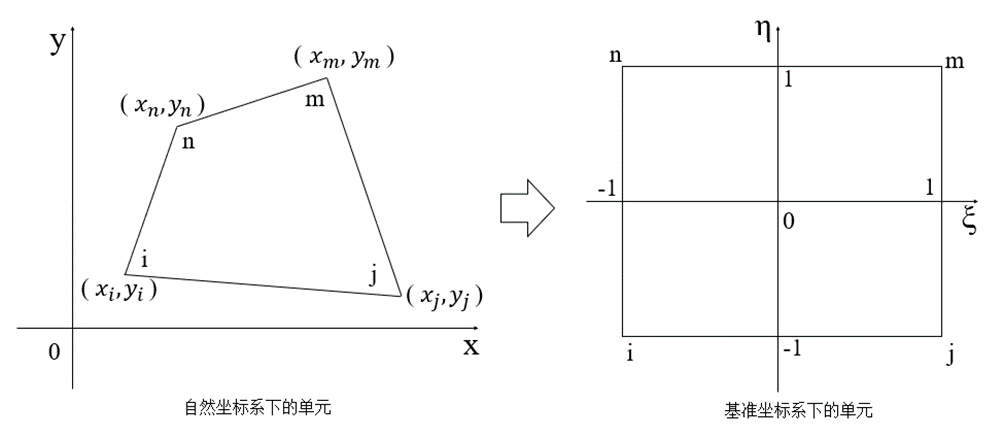
但是我感觉这样映射其实没啥用，除了去掉了量纲，一种更常见的映射如图 3 所示：

图3 自然坐标系到基准坐标系下的映射示例图

这一点在《有限单元法》-- 王勖成 第二章中尚未提到，是胡老师讲过之后我才知道，顺带搜了一下，其思想在于：让基准单元到每个物理单元之间存在一个映射，比较容易想到的是就是线性映射了，在那篇知乎文章中，映射是这样的：

$$\begin{aligned} & x=\frac{1}{4}[(1-\xi)(1-\eta)x_i+(1+\xi)(1-\eta)x_j+(1+\xi)(1+\eta)x_m+(1-\xi)(1+\eta)x_n]\\ & y=\frac{1}{4}[(1-\xi)(1-\eta)y_i+(1+\xi)(1-\eta)y_j+(1+\xi)(1+\eta)y_m+(1-\xi)(1+\eta)y_n] \end{aligned}$$

根据这个映射，可以将母单元上的四个点一一映射到物理单元上的四个点，注意：$x_i \;,\;(i,j,m,n)$ 是已知的，所以根据母单元的中任意一点坐标 ($\xi,\eta$) 可以求得其在物理单元中的坐标 ($x_0,y_0$) ，反过来也一样。

更进一步，将公式（32）写为矩阵形式：

$$\begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} N_i & 0 & N_j & 0 & N_m & 0 & N_n & 0\\ 0 & N_i & 0 & N_j & 0 & N_m & 0 & N_n \end{bmatrix} \cdot \begin{bmatrix} x_i\\ y_i\\ x_j\\ y_j\\ x_m\\ y_m\\ x_n\\ y_n\\ \end{bmatrix}$$

容易得到，形函数为：

$$\left\{ \begin{aligned} N_i(\xi,\;\eta) &=\frac{1}{4} \cdot (1-\xi)\cdot (1-\eta)\\ N_j(\xi,\;\eta) &=\frac{1}{4} \cdot (1+\xi)\cdot (1-\eta)\\ N_m(\xi,\;\eta) &=\frac{1}{4} \cdot (1+\xi)\cdot (1+\eta)\\ N_n(\xi,\;\eta) &=\frac{1}{4} \cdot (1-\xi)\cdot (1+\eta)\\ \end{aligned} \right.$$

那么，因为之前推导的方程是在原坐标系下，所以现在需要转换到基准坐标系下来

我们当然可以直接求 一个变换 $f$ ，使得：

$$N_i(\xi,\eta) = f\cdot N_i(x,y)$$

但是考虑到：

$$\begin{aligned} & \bold B = \bold L \cdot \bold N & \bold S = \bold D \cdot B = \bold D \cdot L \cdot \bold N \end{aligned}$$

所以不妨更近一步，考虑新 $\bold B$ 与旧 $\bold B$ 矩阵之间的转换

回到方程（16）

$$\{\bold \epsilon \}= \begin{pmatrix} \epsilon_x \\ \epsilon_y \\ \gamma_{xy} \end{pmatrix}= \bold L \cdot \bold u= \underbrace{ \begin{bmatrix} \frac{\partial}{\partial x} & 0\\ 0 & \frac{\partial}{\partial y}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y}\\ \end{bmatrix} \cdot \bold N }_{\bold B} \cdot \bold a^e =\bold B\cdot \bold a^e$$

由于坐标系发生了变化，所以我们现在需要求在基准坐标系下的应变

根据链式法则：

$$\frac{\partial f}{\partial \xi} = \frac{\partial f}{\partial x} \cdot \frac{\partial x}{\partial \xi} + \frac{\partial f}{\partial y} \cdot \frac{\partial y}{\partial \xi}\\ \frac{\partial f}{\partial \eta} = \frac{\partial f}{\partial x} \cdot \frac{\partial x}{\partial \eta} + \frac{\partial f}{\partial y} \cdot \frac{\partial y}{\partial \eta}\\$$

求解上式得到：

$$\begin{aligned} & \frac{\partial}{\partial x} = \frac{1}{\det[\bold J]}\left[ \frac{\partial x}{\partial \eta}\cdot\frac{\partial}{\partial \xi} - \frac{\partial x}{\partial \xi}\cdot\frac{\partial}{\partial \eta} \right]\\ & \frac{\partial}{\partial y} = \frac{1}{\det[\bold J]}\left[ \frac{\partial y}{\partial \xi}\cdot\frac{\partial}{\partial \eta} - \frac{\partial y}{\partial \eta}\cdot\frac{\partial}{\partial \xi} \right]\\ \end{aligned}$$

其中 $\bold J$ 为雅克比矩阵，关于对雅克比矩阵的具体描述，请参见：https://www.zhihu.com/question/22739036/answer/442131829

在本文中：

$$\begin{cases} \bold J = \begin{bmatrix} \frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi}\\ \frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta} \end{bmatrix} \\ \det [J] =\frac{1}{8}\bold X_c\cdot \begin{bmatrix} 0 & 1-\eta & \eta - \xi & \xi - 1\\ \eta-1 & 0 & \xi+1 & -\xi-1\\ \xi-\eta & -\xi - 1 & 0 & \eta +1\\ 1-\xi & \xi + 1 & -\eta - 1 & 0 \end{bmatrix} \cdot Y_c\;, & 其中:\bold X_c = \begin{pmatrix} x_i\\ x_j\\ x_m\\ x_n \end{pmatrix}^T , \bold Y_c = \begin{pmatrix} y_i\\ y_j\\ y_m\\ Y_n \end{pmatrix} \end{cases}$$

如此，便将原本对 $(x, y)$ 坐标系下的微分算子，通过雅克比矩阵转换到 $(ξ, η)$ 坐标系下了

新的微分算子为：

$$\bold L^{'} = \frac{1}{\det[\bold J]}\cdot \begin{bmatrix} \frac{\partial x}{\partial \eta}\cdot\frac{\partial}{\partial \xi} - \frac{\partial x}{\partial \xi}\cdot\frac{\partial}{\partial \eta} & 0 \\ 0 & \frac{\partial y}{\partial \xi}\cdot\frac{\partial}{\partial \eta} - \frac{\partial y}{\partial \eta}\cdot\frac{\partial}{\partial \xi}\\ \frac{\partial x}{\partial \eta}\cdot\frac{\partial}{\partial \xi} - \frac{\partial x}{\partial \xi}\cdot\frac{\partial}{\partial \eta} & \frac{\partial y}{\partial \xi}\cdot\frac{\partial}{\partial \eta} - \frac{\partial y}{\partial \eta}\cdot\frac{\partial}{\partial \xi} \end{bmatrix}$$

那么，在新的坐标系下：

$$\epsilon = \bold L^{'} \cdot \bold u\\ \bold B(\xi,\eta)= \bold L^{'} \cdot \bold N(\xi,\eta)= \frac{1}{\det[\bold J]}\cdot \begin{bmatrix} \bold B_i & \bold B_j & \bold B_m & \bold B_n \end{bmatrix}$$

七、求解单元刚度矩阵

因为已经转换了坐标系，所以之前的求解单元刚度矩阵的公式就可以更新为：

$$\bold K^e=\iint\limits_{A}\bold B(x,y)^T\cdot \bold D \cdot \bold B(x,y) \cdot t \;\;\mathrm{d}x\mathrm{d}y =\int_{-1}^{1}\int_{-1}^{1}\bold B(\xi,\eta)^T\cdot \bold D \cdot \bold B(\xi,\eta) \cdot t\cdot \left|\bold J \right| \;\mathrm{d}\xi\mathrm{d}\eta$$

同上， $t$ 为单元厚度

要求解此积分，精确解难以获得，可以通过数值积分获取，比较常用的一种数值积分方式为高斯积分

对于如下函数的积分：

$$I = \int_{-1}^{1}y\;\mathrm{d}x$$

假如 $y_i$ 为样本点， $W_i$ 为样本点对应的权值，$n$ 为样本点的个数，可将上式积分写为：

$$I = \int_{-1}^{1}y\;\mathrm{d}x =\sum_{i=1}^{n}W_i\cdot y_i$$

对于二维高斯积分，同理：

$$\begin{aligned} I &= \int_{-1}^{1}\int_{-1}^{1}f(\xi,\eta)\;\mathrm{d}\xi\mathrm{d}\eta\\ &=\int_{-1}^{1}\sum_{i}W_i\cdot f(\xi_i,\eta)\mathrm{d}\eta\\ &=\sum_{j}W_j\left[\sum_{i}W_i\cdot f(\xi_i,\eta_j)\right]\\ &=\sum_{j}\sum_{i}W_iW_j\cdot f(\xi_i,\eta_j)\\ &\end{aligned}$$

查表，可得部分高斯积分样本值和权值

样本点数	样本点值	权值
$1$	$x_1 = 0$	$2$
$2$	$x_1,x_2=±0.577 350 269 189 626$	$1$
$3$	$x_1,x_3=±0.774 596 669 241 483$ $x_2=0$	$5/9$ $8/9$
$4$	$x_1,x_4=±0.861 136 311 594 053$ $x_2,x_3=±0.339 981 043 584 856$	$0.347 854 845 137 454$ $0.652 145 154 862 546$

由于本文是二维积分问题，选四点即可。已知 $x_1 = 0.577 350 269 189 626$ , $x_2 = -0.577 350 269 189 626$

令：

结点序号	坐标值	坐标值	权值
$1$	$ξ_1 = x_2$	$η_1 = x_2$	$W_1=1*1=1$
$2$	$ξ_2 = x_1$	$η_2 = x_2$	$W_2=1*1=1$
$3$	$ξ_3 = x_1$	$η_3 = x_1$	$W_3=1*1=1$
$4$	$ξ_4 = x_2$	$η_4 = x_2$	$W_4=1*1=1$

根据高斯积分，便可将积分问题转变为求和问题：

$$\bold K^e=t\cdot \left|\bold J \right|\cdot\{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ \;\;\;\bold B(\xi_1,\eta_1)^T\cdot \bold D \bold \cdot B(\xi_1,\eta_1)\cdot W_1\\ +\bold B(\xi_2,\eta_2)^T\cdot \bold D \bold \cdot B(\xi_2,\eta_2)\cdot W_2\\ +\bold B(\xi_3,\eta_3)^T\cdot \bold D \bold \cdot B(\xi_3,\eta_3)\cdot W_3\\ +\bold B(\xi_4,\eta_4)^T\cdot \bold D \bold \cdot B(\xi_4,\eta_4)\cdot W_4\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\}$$

八、组装总刚度矩阵

在进行组装之前，我们需要先找到一个变换 $\bold G$ ，能够将单元刚度阵转换到总刚矩阵中。假如该结构的总结点数为 $l$

不难想到，$\bold G$ 的作用是提高阶数，在《有限单元法》中，对其的定义为：

$$\bold a^e = \bold G \bold a^t$$

其中， $\bold a^e$ 为结点自由度（8*1），如果忘了可以翻看本文的最开始那部分， $\bold a^t$ 是整个结构的结点位移列阵（ $2l * 1$），通过此方程，便可以使得单元的结点自由度数和结构的结点自由度数相同。
其中：

$$\bold G\;\; = \begin{bmatrix} 0&0&\cdots & 1 & 0 & \cdots & 0 & 0 & \cdots & 0 & 0& \cdots & 0 & 0& \cdots & 0\\ 0&0&\cdots & 0 & 1 & \cdots & 0 & 0 & \cdots & 0 & 0& \cdots & 0 & 0& \cdots & 0\\ 0&0&\cdots & 0 & 0 & \cdots & 1 & 0 & \cdots & 0 & 0& \cdots & 0 & 0& \cdots & 0\\ 0&0&\cdots & 0 & 0 & \cdots & 0 & 1 & \cdots & 0 & 0& \cdots & 0 & 0& \cdots & 0\\ 0&0&\cdots & 0 & 0 & \cdots & 0 & 0 & \cdots & 1 & 0& \cdots & 0 & 0& \cdots & 0\\ 0&0&\cdots & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 & 1& \cdots & 0 & 0& \cdots & 0\\ 0&0&\cdots & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 & 0& \cdots & 1 & 0& \cdots & 0\\ 0&0&\cdots & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 & 0& \cdots & 0 & 1& \cdots & 0\\ \end{bmatrix}$$

同样的，可以得到：

$$\bold a^t = \bold G^T \bold a^e$$

将上式展开写一下：

$$\bold a^t = \bold G^T \bold a^e = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} u_i \\ v_i \\ u_j \\ v_j \\ u_m \\ v_m \\ u_n \\ v_n\\ \end{bmatrix}\;\; = \begin{bmatrix} 0\\ 0\\ u_i\\ v_i\\ \vdots\\ u_j\\ v_j\\ \vdots\\ u_m\\ v_m\\ \vdots\\ u_n\\ v_n\\ \vdots\\ 0\\ 0\\ \end{bmatrix}$$

从《有限单元法》中可以看到，$\bold G$ 矩阵还可以将单元刚度阵组装到总刚度矩阵中，由于单元刚度阵的维度为8*8，实在太大了不便于展示，所以用分块矩阵来表示，同时，令：

$$\bold i =\begin{bmatrix} 2i-1 & 2i\end{bmatrix}^T \;\;(i,j,m,n)$$

下面的方程会直观的展示组装的过程

$$\begin{aligned} \bold G^T\bold K^e\bold G \; & = \begin{bmatrix} 0&0& 0& 0\\ \vdots & \vdots& \vdots& \vdots\\ \bold I & \bold 0& \bold 0&\bold 0\\ \vdots & \vdots&\vdots &\vdots\\ \bold 0 & \bold I &\bold 0 &\bold 0\\ \vdots & \vdots& \vdots& \vdots\\ \bold 0 & \bold 0 &\bold I &\bold 0\\ \vdots & \vdots& \vdots& \vdots\\ \bold 0 & \bold 0 &\bold 0 &\bold I\\ \vdots & \vdots& \vdots& \vdots\\ 0&0& 0& 0\\ \end{bmatrix} \begin{bmatrix} \bold K_{ii} & \bold K_{ij} & \bold K_{im} & \bold K_{in}\\ \bold K_{ji} & \bold K_{jj} & \bold K_{jm} & \bold K_{jn}\\ \bold K_{mi} & \bold K_{mj} & \bold K_{mm} & \bold K_{mn}\\ \bold K_{ni} & \bold K_{nj} & \bold K_{nm} & \bold K_{nn}\\ \end{bmatrix} \begin{bmatrix} 0&\cdots&\bold I&\cdots&\bold 0&\cdots&\bold 0&\cdots&\bold 0&\cdots&0\\ 0&\cdots&\bold 0&\cdots&\bold I&\cdots&\bold 0&\cdots&\bold 0&\cdots&0\\ 0&\cdots&\bold 0&\cdots&\bold 0&\cdots&\bold I&\cdots&\bold 0&\cdots&0\\ 0&\cdots&\bold 0&\cdots&\bold 0&\cdots&\bold 0&\cdots&\bold I&\cdots&0\\ \end{bmatrix} \\ & = \begin{bmatrix} 0& \cdots & 0&\cdots& 0&\cdots& 0&\cdots& 0&\cdots& 0\\ \vdots && \vdots &&\vdots &&\vdots && \vdots &&\vdots\\ 0& \cdots &\bold K_{ii}&\cdots& \bold K_{ij}&\cdots&\bold K_{im}&\cdots& \bold K_{in}&\cdots&0\\ \vdots && \vdots &&\vdots &&\vdots && \vdots &&\vdots\\ 0& \cdots &\bold K_{ji}&\cdots& \bold K_{jj}&\cdots&\bold K_{jm}&\cdots& \bold K_{jn}&\cdots&0\\ \vdots && \vdots &&\vdots &&\vdots && \vdots &&\vdots\\ 0& \cdots &\bold K_{mi}&\cdots& \bold K_{mj}&\cdots&\bold K_{mm}&\cdots& \bold K_{mn}&\cdots&0\\ \vdots && \vdots &&\vdots &&\vdots && \vdots &&\vdots\\ 0& \cdots &\bold K_{ni}&\cdots& \bold K_{nj}&\cdots&\bold K_{nm}&\cdots& \bold K_{nn}&\cdots&0\\ \vdots && \vdots &&\vdots &&\vdots && \vdots &&\vdots\\ 0& \cdots &0&\cdots& 0&\cdots&0&\cdots& 0&\cdots&0\\ \end{bmatrix} \end{aligned}$$

细心的同学一定会发现， $G^T$ 似乎有些问题，我在推的时候也发现了，如果按照严格的转置定义去推导，得到的总刚矩阵顺序会被上下颠倒，读者可以自行尝试推导，《有限单元法》一书中也是这样写的，并且没有对 $G\; 和\; G^T$ 区别于严格的转置定义这一点进行说明。

如此，便可以将单元刚度阵组装到总刚度阵中了。

九、加载结点荷载列阵

假如单元荷载矩阵为：

$$\bold P^e = \begin{bmatrix} \bold P_i & \bold P_j & \bold P_m & \bold P_n \end{bmatrix}^T \;\;其中， \bold P_i =(P^{\xi}_i ,\; P^{\eta}_i )^T \;\;(i,j,m,n)$$

那么，将单元荷载阵加载到总结点荷载阵也是通过 $\bold G$ 矩阵实现的

$$\bold G^T \bold P^e = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} P^{\xi}_i\\ P^{\eta}_i\\ P^{\xi}_j\\ P^{\eta}_j\\ P^{\xi}_m\\ P^{\eta}_m\\ P^{\xi}_n\\ P^{\eta}_n\\ \end{bmatrix} \;\; = \begin{bmatrix} 0\\ 0\\ \vdots\\ P^{\xi}_i\\ P^{\eta}_i\\ \vdots\\ P^{\xi}_j\\ P^{\eta}_j\\ \vdots\\ P^{\xi}_m\\ P^{\eta}_m\\ \vdots\\ P^{\xi}_n\\ P^{\eta}_n\\ \vdots\\ 0\\ 0\\ \end{bmatrix}$$

注意：以上只是理论上的推导，这样做消耗了很多内存和时间，在实际编程过程中，在计算得到了单元刚度阵和荷载阵后，只需要按照单元的结点自由度编码，“对号入座”地叠加到总刚度矩阵和总结点荷载阵中的相应位置即可

十、处理位移约束条件

位移约束条件也可以称为边界条件，对于一个结构来说，当有外力作用于某些单元时，那么它一定会产生运动，但是有限元分析希望得到的是当结构平衡之后，结构发生了哪些变化，如果没有约束，那么它永远也达到不了平衡，表现在方程中，就是总刚矩阵是奇异的，会得到无穷多个解，所以，结构一般就是有约束的，具体表现在结构一端固定在某些不会发生移动的物体上，比如结构中有一道梁固定在墙壁上，而我们假设墙壁是不会动的，那么固定在墙壁上的梁所对应的结点的位移就一定是0，处理位移约束条件，就是要把这种位移一定为0的条件体现到方程中，当然，位移也不一定非得是0，比如结构的一端连接在一根绳子上，而假设绳子是不会断的，那么与绳子想连的结点的位移就是一个非零定值，以下三种方法将依次讨论这些情况。

1、直接代入法

在那个天津大学的PPT中，对其的描述是这样的：若第 r 个自由度方向位移分量为0，则将整体刚度矩阵第 r 行，第 r 列划掉，后一行上移，右一列左移，这样总刚减少一阶，未知数减少一个。当时看到后非常惊讶，真的可以这样直接划掉吗，而且也降低了阶数，那还要其他方法干啥呢，但是回头一想：这么简单直接的方法为啥老师没讲呢，就带着疑问看了一下《有限单元法》中的相关部分。

在《有限单元法》中，对其的严格定义如下：

将原方程组重新组合为：

$$\begin{bmatrix} \bold K_{aa}& \bold K_{ab}\\ \bold K_{ba}& \bold K_{bb} \end{bmatrix} \begin{bmatrix} \bold a_a\\ \bold a_b \end{bmatrix} =\begin{bmatrix} \bold P_a\\ \bold P_b \end{bmatrix}$$

其中，$\bold a_a$ 为待定结点位移，$\bold a_b$ 为已知结点位移；而且 $\bold K_{aa}, \;\bold K_{ab}, \;\bold K_{ba},\; \bold K_{bb}, \;\bold P_a,\; \bold P_b$ 等为与其相应的刚度矩阵和载荷矩阵的分块矩阵。由刚度矩阵的对称性可知 $\bold K_{ba} = \bold K_{ab}^T$ 。

由公式（48）可知：

$$\bold K_{aa}\cdot \bold a_a + \bold K_{ab} \cdot \bold a_b = \bold P_a$$

由于 $\bold K_{ab},\;\bold a_b$ 为已知，最后的求解方程可以写为

$$\bold K^{*}\cdot \bold a^{*} = \bold P^*$$

其中： $\bold K^*=\bold K_{aa},\;\bold a^*=\bold a_a,\; \bold P^*=\bold P_a-\bold K_{ab}\cdot \bold a_b$

若总体结点位移为 $n$ 个，其中有已知结点位移 $m$ 个，则得到一组求解$n-m$个待定结点位移的修正方程组， $\bold K^*$ 为 $n - m$ 阶方阵。修正方程组的意义是在原来 $n$ 个方程中，只保留与待定（未知的）结点位移相应的 $n - m$ 个方程，并将方程中左端的已知位移和相应刚度系数的乘积（已知）移动至方程右端作为载荷修正项。

但是，这种方法需要重新组合方程，组成的新方程的阶数确实降低了，但是结点位移的顺序性已经被破坏了，对编写程序造成困难。

2、对角元素置一法

当给定位移值是零位移时，可以在刚度矩阵（或者称之为方程的系数矩阵） $\bold K$ 中与零结点位移相对应的行列中，将主对角元素改为1，其他元素改为0；在载荷列阵中将与零结点位移相对应的元素改为0即可。例如有 $a_j=0$ ，则对方程系数矩阵 $\bold K$ 的第 $j$ 行，第 $j$ 列及载荷阵第 $j$ 个元素作如下修改：

$$\begin{bmatrix} K_{11}&K_{12}&\cdots\cdots&0&\cdots\cdots&K_{1n}\\ K_{21}&K_{22}&\cdots\cdots&0&\cdots\cdots&K_{2n}\\ \vdots & \vdots&& \vdots&& \vdots\\ \vdots & \vdots&& \vdots&& \vdots\\ \hdashline 0 & 0 &\cdots\cdots& 1& \cdots\cdots&0\\ \hdashline \vdots & \vdots&& \vdots&& \vdots\\ \vdots & \vdots&& \vdots&& \vdots\\ K_{n1}&K_{n2}&\cdots\cdots&0&\cdots\cdots&K_{nn}\\ \end{bmatrix} \begin{bmatrix} a_1\\ a_2\\ \vdots\\ \vdots\\ a_j\\ \vdots\\ \vdots\\ a_n \end{bmatrix} \;\; = \begin{bmatrix} p_1\\ p_2\\ \vdots\\ \vdots\\ 0\\ \vdots\\ \vdots\\ p_n \end{bmatrix}$$

这样修正后，解方程则可得 $a_j=0$。对多个给定零位移则依次修正，全部修正完毕后再求解。用这种方法引入强制边界条件比较简单，不改变原来方程的阶数和结点位移的编号顺序，但这种方法只能用于给定零位移的情况。

3、对角元素乘大数法

当有结点位移为给定值 $a_j = a_j^*$ 时，第 $j$ 个方程进行如下修改：对角元素 $K_{jj}$ 乘以大数 $\alpha$ ( $\alpha$ 可取 $10^{10}$ 左右量级)，并将 $P_j$ 用 $\alpha K_{jj}a^*_j$ 取代，即：

$$\begin{bmatrix} K_{11}&K_{12}&\cdots\cdots&K_{1j}&\cdots\cdots&K_{1n}\\ K_{21}&K_{22}&\cdots\cdots&K_{2j}&\cdots\cdots&K_{2n}\\ \vdots & \vdots&& \vdots&& \vdots\\ \vdots & \vdots&& \vdots&& \vdots\\ K_{j1} & K_{j2} &\cdots\cdots&\{ \alpha\cdot K_{jj} \}& \cdots\cdots&K_{jn}\\ \vdots & \vdots&& \vdots&& \vdots\\ \vdots & \vdots&& \vdots&& \vdots\\ K_{n1}&K_{n2}&\cdots\cdots&K_{nj}&\cdots\cdots&K_{nn}\\ \end{bmatrix} \begin{bmatrix} a_1\\ a_2\\ \vdots\\ \vdots\\ a_j\\ \vdots\\ \vdots\\ a_n\\ \end{bmatrix} = \begin{bmatrix} P_1\\ P_2\\ \vdots\\ \vdots\\ \{\alpha\cdot K_{jj}\cdot a_j^*\}\\ \vdots\\ \vdots\\ P_n\\ \end{bmatrix}$$

经过修改后的第 $j$ 个方程为：

$$K_{j1}\cdot a_1 + K_{j2}\cdot a_2 + \cdots + \alpha\cdot K_{jj}\cdot a_j + \cdots + K_{jn}\cdot a_n = \alpha\cdot K_{jj}\cdot a_j^*$$

由于 $\alpha \cdot K_{jj}\gg K_{ji} (i \neq j)$ ，方程左端的 $\alpha\cdot K_{jj}\cdot a_j$ 项相较于其他项要大很多，因此可以近似得到：

$$\alpha\cdot K_{jj}\cdot a_j \approx \alpha\cdot K_{jj}\cdot\overline a_j$$

则有：

$$a_j = \overline a_j$$

对于多个给定位移 ( $j=c_1, \; c_2,\; \cdots\;,c_l$ ) 时，则按顺序将每个给定位移都作上述修正，得到全部修正后的 $\bold K$ 和 $\bold P$ ，然后解方程即可得到包括给定位移在内的全部结点位移值。此方法使用简单，对任何给定位移（零值或非零值）都适用。采用这种方法引入强制边界条件时方程的阶数不变，结构不变，结点位移的顺序也不变，因此经常在有限元法中采用。

---

1. 这段话来自知乎：https://zhuanlan.zhihu.com/p/363678419 ↩︎